Güneş Sistemi; bir adet yıldız, 8 gezegen ve 150 uydudan oluşmaktadır. Bir de 5 cüce gezegen ve onların 8 uydusu yer almakta. Tüm bu gök cisimleri belirli bir düzende, belirli yörüngelerinde hareket etmektedir. Bu gezegenlerin hareketleri tarih boyunca farklı bilim insanları tarafından açıklanmaya çalışılmıştır. Ancak bunlardan sadece tek bir açıklama doğruluğunu ispat etmiştir: Kepler yasaları...

16. yüzyılda Danimarkalı aristokrat ve gökbilimci Tycho Brahe, sadece çıplak gözle astronomik gözlemler yapmıştır. Asıl adı Tyge Ottesen Brahe olan gökbilimci Kopernik’in ölümünden üç sene sonra doğmuştur. Yani tam da astronomik gelişmelerin en yoğun yaşandığı dönemlerden birinde dünyaya gelmiştir. Bu sayede küçük yaşlardan beri astronomiye ilgi duymuştur. 1559’da Kopernik Üniversitesi’nde güneş tutulmasını gözlemledi ve tutkuyla astronomiye bağlandı. Ancak amcasının isteği üzerine siyasal bilime yönelmiş ve aristokrat olmuştu. Zamanla gökyüzünü gözlemledi ve bu gözlemleriyle bir sürü hesaplamalar ortaya koydu.

Brahe Alman İmparatorluğu’nun astroloğuyken o güne kadar hazırlanmış en iyi gök haritasını hazırlamıştır. Kepler o dönemlerde Brahe’nin kalfasıydı. Brahe’nin ölümünden sonra Kepler, o meşhur gök haritasını inceledi ve gezegenlerin konumlarıyla hareketlerinin üç basit matematiksel bağıntı ile açıklanabildiğini gördü. Ve günümüzde bu bağıntılar Kepler yasaları olarak geçmektedir.

1. Yasa

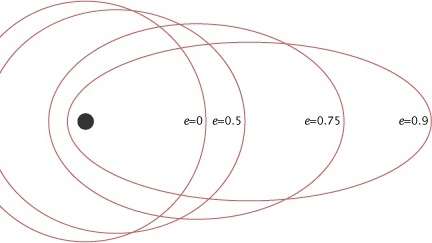
Tanım: Her gezegen, odak noktalarının birinde Güneş’in bulunduğu bir eliptik yörünge üzerinde hareket eder. Keplerin bu 1. yasasını ortaokul çağlarımızdan beri biliyoruz. Ve daha basit bir tabirle gezegenlerin, Güneş etrafında eliptik bir yörünge üzerinde hareket ettiği çıkarımını yapabiliriz. Gezegenlerin yörüngeleri var ancak bu yörüngeler çembersel değil eliptiktir. Eliptik yörünge demek, astronomi ve uzay mühendisliğine göre, basıklığı 0 ile 1 arasında olan yörüngedir. Dünyamız da Güneş çevresinde eliptik bir yörüngede hareket etmektedir. Ancak bu yörünge üzerindeki konumunda bir eğiklik söz konusudur. Buna eksen eğikliği denir ve 23 derece, 27 dakikadır. Bu eğiklik insanoğlunun yaşamının en önemli etmenlerinden biridir. Bu durum mevsimlerin oluşmasına sebebiyet verir.

2. Yasa

Tanım: Bir gezegeni Güneş’e bağlayan sanal çizgi eşit zaman aralıklarında eşit alan tarar. Bu yasanın kafanızda iyice yer etmesi adına şu şekilde düşünebilirsiniz: M kütleli bir yıldız düşünün. Bu yıldız etrafında da m kütleli bir gezegen elips yörüngede hareket ediyor olsun. Şimdi bu m kütleli gezegenden, M kütleli yıldıza bir ip atın. Yani gezegen ve yıldız bir iple bağlandı. Şimdi 0. saniyeden, 2. saniyeye kadar sistemi çalıştıralım. Ancak gezegenimiz 0. saniyede yıldızdan en uzak konumda olacak (Eliptik bir yörüngemiz olduğunu unutmayın.). Gezegen hareket halinde iken yıldıza bağlanmasını sağlayan ip de hareket edecek ve 2 saniye boyunca belirli bir alanı tarayacak.

Şimdi bir de aynı şeyleri yıldıza en yakın olan konumda gerçekleştirelim. Ve yine 0. ve 2. saniyeler arasında sistemi çalıştıralım. Şimdi elimizde eliptik bir çemberde taranmış iki farklı alan var. Şimdi de işin matematiksel izahına bakalım. (Burada şunu unutmamalısınız ki taranan alanların şekilleri çok farklı. Gözlemlediğiniz zaman alanların hesaplama sonuçlarının birbirlerine yakın çıkıp çıkmayacağı konusunda kararsız kalabilirsiniz.)

Burada matematiksel izah için bilmemiz gereken alansal hızın formülüdür. Formül ½.(r^2).(z)’dir. Şimdi bu bağıntının zamana göre türevini alalım. 

d/dt.[ ½.(r^2).(z)]=0 

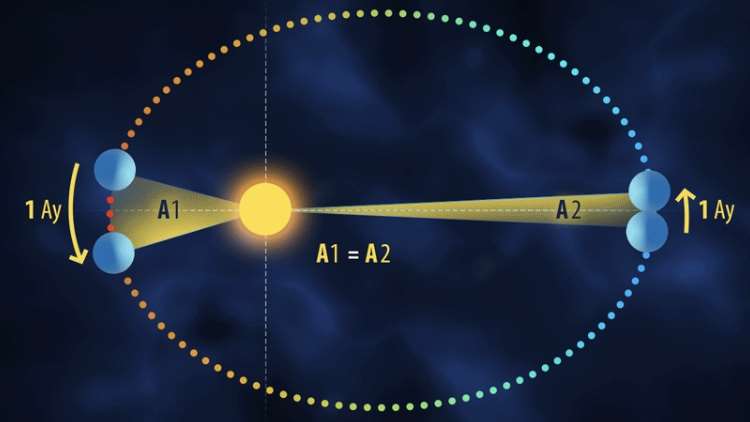
Gördüğünüz gibi zamana göre türevi alınca sıfır sayısına yani bir sabite ulaşıyoruz. Ve bu şu demek oluyor: Gezegen tarafından birim zamanda taranan alan sabittir. Ve bunun her birim zamanda meydana geldiği düşünülürse hangi zaman aralığı olursa olsun karşılaşmada eşit alanların tarandığını göreceğiz. Yalnız tek şart eşit zaman aralığında olması.

3. Yasa

Tanım: Bir gezegenin yörüngesel periyodunun karesi, dolmadığı elipsin ana eksen küpü ile doğru orantılıdır. Bir gezegenin periyodu demek örnek vererek açıklamak gerekirse Dünya’nın Güneş etrafında bir tam tur atması sonucunda geçen süredir. Yasada bu kısım P ile gösterilir. Eliptik yörüngenin ana ekseni ise yıldızdan veya merkezi odak noktada en uzak noktadır. Ve bu da yasada alfa işareti ile gösterilir. Biz bunu “a” ile sembol edeceğiz. Eğer matematiksel izaha gelecek olursak şu ifadeyi verebiliriz: P^2 ile a^3 doğru orantılıdır. Ancak iş bu kadar basit değil. Hem bu ifade tek başına bir işimize de yaramıyor. Şimdi şu bağıntıya bir bakalım;

P^2(gezegen)/a^3(gezegen) ifadesi ile P^2(Dünya)/a^3(Dünya) ifadesi birbirine eşittir.

Şimdi bu ifade sayesinde bir eşitlik elde ettik. Peki bu eşitlik neye işaret ediyor? Buradan biz bir sabite gidiyoruz. C sabiti…

C=2,97473.(10^-19).sn^2.m^-3

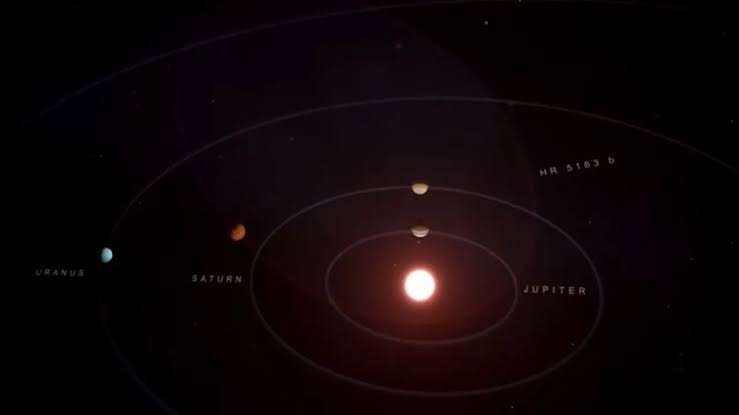
Yukarıda verilen bağıntıyı bir örnek içerisinde işleyelim. A ve B gezegenleri olsun. Bunlar aynı sistem üzerinde. A gezegeni Güneş’e 4r uzaklıkta iken B gezegeni r uzaklığındadır. Bu durumda A gezegeninin hızı v, B’ninki de 2v oluyor. Ayrıca B gezegeni x kadar yol alırken A gezegeni 4x kadar yol alacaktır. Tim bu değerleri bağıntıda yerine koyarsak eğer B gezegeni t sürede yörüngeyi dolanırken A gezegeni 8t sürede dolanacaktır.